Tam giác đều là một hình học cơ bản trong toán học và được ứng dụng trong nhiều lĩnh vực khác nhau. Việc tính diện tích tam giác đều giúp hiểu sâu hơn về tính chất hình học và có ý nghĩa quan trọng trong thực tiễn. Trong bài viết này của FPT Shop, chúng ta sẽ khám phá chi tiết về tam giác đều, cách tính diện tích tam giác đều và những ứng dụng thực tế của công thức này.
Tam giác đều là gì?
Tam giác đều là một tam giác có các góc bằng nhau (60 độ) và các cạch cũng bằng nhau. Đây là loại tam giác đặc biệt với tính đối xứng hoàn hảo. Mỗi đỉnh của tam giác đều cách đều các đỉnh còn lại và chia mặt phẳng thành ba phần bằng nhau. Vì tính đối xứng và đơn giản, tam giác đều thường xuất hiện trong nhiều bài toán hình học cơ bản và ứng dụng thực tiễn.

Cách tính diện tích tam giác đều
Cách tính diện tích tam giác đều sẽ dựa vào công thức tính diện tích tam giác bất kỳ.
Diện tích của một tam giác bất kỳ được tính bằng công thức:
- S= 1/2 x a x h.
Trong đó:
- S là diện tích tam giác.
- a là độ dài cạnh đáy (cạnh tam giác).
- h là chiều cao tương ứng với cạnh đáy.
Ví dụ: Tính diện tích của tam giác đều có cạnh dài 6 cm và đường cao 10 cm.
- Độ dài cạnh tam giác: a = 6 cm.
- Đường cao của tam giác: h = 10 cm.
Áp dụng công thức cách tính diện tích tam giác đều như sau:
- S= 1/2 x 6 x 10 = 60/2 = 30 cm².
Vậy, diện tích của tam giác đều có cạnh 6 cm và đường cao 10 cm là 30 cm².
Trường hợp chỉ biết chiều dài cạnh
Nếu bạn chỉ biết chiều dài cạnh của tam giác, bạn có thể vẽ một đường thẳng từ đỉnh tam giác đến trung điểm của cạnh đáy để tạo thành đường cao. Đường cao này sẽ chia cạnh đáy thành hai phần bằng nhau. Khi đó, bạn có thể sử dụng định lý Pythagore
(a² + b² = c²) để tính đường cao, sau đó áp dụng công thức tính diện tích tam giác đều như đã nêu trước đó.Hoặc, để đơn giản và tiết kiệm thời gian, bạn có thể dùng ngay công thức tính nhanh:
- S= a² √3/4.
Điều này có nghĩa là bạn lấy bình phương chiều dài cạnh của tam giác đều, nhân với √3, rồi chia cho 4 để tính diện tích.
Ví dụ:
Tính diện tích tam giác ABC có 3 cạnh bằng nhau, mỗi cạnh dài 6 cm.
Vì tam giác ABC có 3 cạnh bằng nhau, nên đó là tam giác đều. Áp dụng công thức trên, ta có diện tích tam giác ABC bằng:
- S= 6² √3/4 = 15.6 cm².
Trường hợp đề yêu cầu tính đường cao của tam giác đều
Ngoài việc tính diện tích, đề bài cũng có thể yêu cầu bạn tính đường cao của tam giác đều. Trước khi giải quyết, bạn cần hiểu rõ tính chất của đường cao trong tam giác đều:
- Đường cao của tam giác đều là đoạn thẳng từ một đỉnh của tam giác đến trung điểm của cạnh đối diện và vuông góc với cạnh đó.
- Trong tam giác đều, ba đường cao có độ dài bằng nhau và giao nhau tại một điểm duy nhất - trọng tâm của tam giác. Điểm này cũng là giao điểm của các đường phân giác, đường trung trực và đường trung tuyến.
- Để tính chiều dài đường cao của tam giác đều, bạn có thể sử dụng công thức: chính là độ dài cạnh của tam giác đều.
Ví dụ:
Tính chiều dài đường cao AH của tam giác đều ABC, biết AB dài 5 cm.
Áp dụng công thức trên, chúng ta có kết quả như sau:
- AH = 5² √3/2 ≈ 4.33cm
Xem thêm: Cách tính diện tích hình vuông và hướng dẫn làm một số dạng bài tập thường gặp nhất
Ứng dụng thực tế của việc tính diện tích tam giác đều
Tính diện tích tam giác đều không chỉ là một bài toán toán học thuần túy mà còn có ứng dụng thực tế rộng rãi trong nhiều lĩnh vực.
1. Trong kiến trúc và thiết kế
Trong nhiều công trình kiến trúc, tam giác đều được sử dụng để tạo ra các kết cấu vững chắc và có tính thẩm mỹ cao. Việc tính toán chính xác diện tích tam giác đều giúp các kiến trúc sư phân chia không gian hiệu quả, đặc biệt là trong việc thiết kế các tòa nhà có mái vòm tam giác hoặc các kiến trúc hình tam giác đều phức tạp.

2. Trong kỹ thuật và xây dựng
Công thức tính diện tích tam giác đều còn rất hữu ích trong lĩnh vực kỹ thuật và xây dựng. Khi xây dựng các kết cấu hình tam giác, như mái nhà hoặc giàn giáo, việc tính toán diện tích tam giác đều giúp tính toán được lượng vật liệu cần thiết cho thi công, tối ưu chi phí, nhân lực và thời gian.

3. Thiết kế đồ họa và nghệ thuật sáng tạo
Việc tính toán diện tích tam giác đều giúp các nhà thiết kế cân đối hình ảnh và không gian một cách hài hòa, tạo nên các sản phẩm thiết kế tinh tế và độc đáo.
4. Trong giáo dục
Trong chương trình học toán ở các trường học, việc tính diện tích tam giác đều là một phần quan trọng giúp học sinh hiểu về hình học và các công thức toán học cơ bản. Bài toán này giúp học sinh phát triển kỹ năng tư duy logic và giải quyết vấn đề thực tiễn.
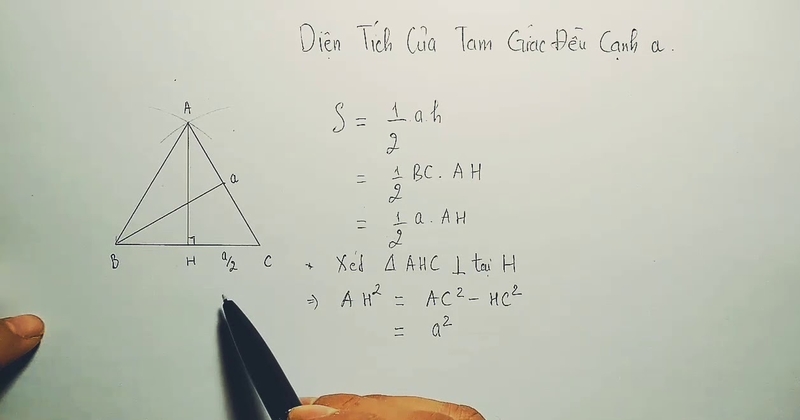
Những lưu ý khi tính diện tích tam giác đều
Khi tính diện tích tam giác đều, bạn cần lưu ý một số điểm sau để đảm bảo kết quả chính xác:
- Đảm bảo đúng độ dài cạnh: Độ dài cạnh là yếu tố quan trọng nhất trong công thức tính diện tích tam giác đều. Hãy đảm bảo rằng bạn đo chính xác chiều dài của các cạnh trước khi áp dụng công thức.
- Sử dụng đúng đơn vị đo lường: Khi tính diện tích tam giác đều, đảm bảo rằng các đơn vị đo của cạnh và kết quả diện tích đều cùng một hệ thống đơn vị (cm, m, inch, v.v.).
- Áp dụng công thức đúng cách: Hãy đảm bảo rằng bạn hiểu rõ từng yếu tố trong công thức trước khi thực hiện phép tính.

Tạm kết
Cách tính diện tích tam giác đều là một trong những kiến thức cơ bản trong toán học nhưng lại có nhiều ứng dụng thực tiễn trong đời sống và công việc. Từ việc thiết kế kiến trúc đến tối ưu hóa chi phí trong xây dựng, việc tính diện tích tam giác đều giúp giải quyết nhiều vấn đề quan trọng. Hy vọng qua bài viết này, bạn đã hiểu rõ hơn về cách tính diện tích tam giác đều và những ứng dụng thực tế của tam giác đều.
Hiện nay có rất nhiều ứng dụng tính toán trên điện thoại, giúp bạn thực hiện các phép tính từ cơ bản đến phức tạp chỉ trong vài giây. Nếu bạn đang tìm kiếm một chiếc smartphone mạnh mẽ, hỗ trợ tốt cho các nhu cầu học tập, làm việc và giải trí, hãy đến ngay FPT Shop nhé.
Mua ngay iPhone tại FPT Shop để nhận ưu đãi và chế độ bảo hành uy tín:
- iPhone.
Xem thêm:
- Công thức tính diện tích hình thang và 4 lưu ý quan trọng khi làm các dạng bài tập liên quan
- Khám phá công thức tính diện tích hình chữ nhật nhanh gọn và chính xác nhất